Phonetic algorithms

Intro

A phonetic algorithm matches two different words with similar pronunciation to the same code, which allows phonetic similarity based word set comparison and indexing.

Often it is quite difficult to find atypical name (or surname) in the database, for example:

— Hey, John, look for Adolf Schwarzenegger.
— Adolf Shwardseneger? There is no such person!

In this case, the use of phonetic algorithms (especially in combination with fuzzy matching algorithms) can significantly simplify the problem.

These algorithms are very useful for searching in lists of people in databases, as well as for using in a spell checker. They are often used in combination with the algorithms of fuzzy search, providing users with a handy search by name and surname in databases, lists of people and so on.

In this article I will discuss the most well-known algorithms, such as Soundex, Daitch-Mokotoff Soundex, NYSIIS, Metaphone, Double Metaphone, Caverphone.

Soundex

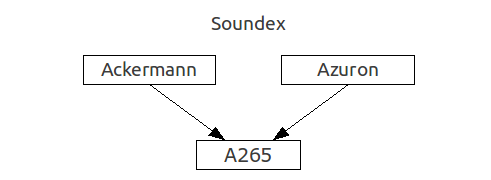
One of the first algorithms was Soundex invented in the 1910s by Robert Russell. This algorithm (its American version) matches words to the numerical index like A126. Its working principle is based on the partition of consonants in groups with ordinal numbers, which are then compiled to the resulting value. Later several improvements was suggested.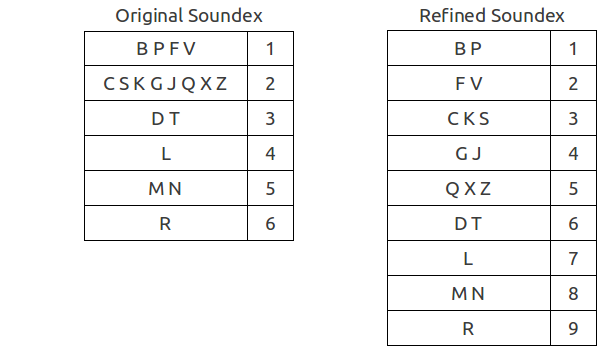



The first letter is stored, subsequent letters are matched to digits by the table above. Letters that are not listed in the table (all the vowels and some consonants) are ignored. Adjacent letters, or letters from the same group separated by H or W are written as one letter. The result is truncated to 4 characters. Missing positions contain zeros. It is easy to see that after all these procedures there is only 7000 different values of that code, which results in a set of unliked words with the same Soundex code. Thus, in most cases the result involves a large number of "false positive" values.



As you can see in the refined soundex the letters are divided into more groups. In addition, there are no special cases with H and W, they are simply ignored. Also length of the result is not truncated, so the code does not have a fixed length.

Examples

Original Soundex:
F234 → Fusedale.
G535 → Genthner, Gentner, Gianettini, Gunton.
G640 → Garlee, Garley, Garwell, Garwill, Gerrell, Gerrill, Giral, Gorelli, Gorioli, Gourlay, Gourley, Gourlie, Graal, Grahl, Grayley, Grealey, Greally, Grealy, Grioli, Groll, Grolle, Guerola, Gurley.
H326 → Hadcroft, Hadgraft, Hatchard, Hatcher, Hatzar, Hedger, Hitscher, Hodcroft, Hutchcraft.
P630 → Parade, Pardew, Pardey, Pardi, Pardie, Pardoe, Pardue, Pardy, Parradye, Parratt, Parrett, Parrot, Parrott, Pearde, Peart, Peaurt, Peert, Perdue, Peret, Perett, Perot, Perott, Perotti, Perrat, Perrett, Perritt, Perrot, Perrott, Pert, Perutto, Pirdue, Pirdy, Pirot, Pirouet, Pirt, Porrett, Porritt, Port, Porte, Portt, Prate, Prati, Pratt, Pratte, Pratty, Preddy, Preedy, Preto, Pretti, Pretty, Prewett, Priddey, Priddie, Priddy, Pride, Pridie, Pritty, Prott, Proud, Prout, Pryde, Prydie, Purdey, Purdie, Purdy.

Refined Soundex:
B1905 → Braz, Broz
C30908 → Caren, Caron, Carren, Charon, Corain, Coram, Corran, Corrin, Corwin, Curran, Curreen, Currin, Currom, Currum, Curwen
H093 → Hairs, Hark, Hars, Hayers, Heers, Hiers
L7081096 → Lambard, Lambart, Lambert, Lambird, Lampaert, Lampard, Lampart, Lamperd, Lampert, Lamport, Limbert, Lombard
N807608 → Nolton, Noulton

One Soundex code value is matched for 21 surnames. In the case of an refined version of Soundex, 2-3 names match to the same code.

NYSIIS

Developed in 1970 as part of the "New York State Identification and Intelligence System", this algorithm gives better results relatively to the original Soundex using more sophisticated rules for transforming the original word to the result code. This algorithm is designed to work specifically with American names.

NYSIIS computation algorithm

1. Transform the beginning of the word using the following rules:
   MAC → MCC
   KN → N
   K → C
   PH, PF → FF
   SCH → SSS
2. Transform the ending of the word using the following rules:
   EE → Y
   IE → Y
   DT, RT, RD, NT, ND → D
3. Transform all letters except first using the rules below:
   EV → AF
   A, E, I, O, U → A
   Q → G
   Z → S
   M → N
   KN → N
   K → C
   SCH → SSS
   PH → FF
   After a vowel: remove H and transform W → A
4. Remove S at the end
5. Transform AY at the end → Y
6. Remove A at the end
7. Truncate word to 6 letters (optional).

Examples

DAGAL → Diggell, Dougal, Doughill, Dougill, Dowgill, Dugall, Dugall.
GLAND → Glinde.
PLANRAG → Plumridge.
SANAC → Chinnick, Chinnock, Chinnock, Chomicki, Chomicz, Schimek, Shimuk, Simak, Simek, Simic, Sinnock, Sinnocke, Sunnex, Sunnucks, Sunock.
WABARLY → Webberley, Wibberley.

NYSIIS matches to the same code a bit more than two surnames.

Daitch-Mokotoff Soundex

This algorithm was developed by two genealogist, Gary Mokotoff and Randy Daitch in 1985. They tried to achieve the best results with Eastern European (including Russian, Jewish) surnames.
This algorithm has little in common with the original Soundex, except that the result is still a sequence of digits. But now the first letter is also encoded as a digit.

It has a much more complicated conversion rules. Calculation of resulting code is also involves not only single characters, but the groups of characters. In addition, the result of the form 023689 provides about 600 000 different values of that code. This feature coupled together with complex rules reduces the number of "false positive" words in the result set.

Transformations are performed using the table below. The order of conversions is the order of letter combinations in the table.

Letter combination	At the start	After a vowel	Other
AI, AJ, AY, EI, EY, EJ, OI, OJ, OY, UI, UJ, UY	0	1
AU	0	7
IA, IE, IO, IU	1
EU	1	1
A, UE, E, I, O, U, Y	0
J	1	1	1
SCHTSCH, SCHTSH, SCHTCH, SHTCH, SHCH, SHTSH, STCH, STSCH, STRZ, STRS, STSH, SZCZ, SZCS	2	4	4
SHT, SCHT, SCHD, ST, SZT, SHD, SZD, SD	2	43	43
CSZ, CZS, CS, CZ, DRZ, DRS, DSH, DS, DZH, DZS, DZ, TRZ, TRS, TRCH, TSH, TTSZ, TTZ, TZS, TSZ, SZ, TTCH, TCH, TTSCH, ZSCH, ZHSH, SCH, SH, TTS, TC, TS, TZ, ZH, ZS	4	4	4
SC	2	4	4
DT, D, TH, T	3	3	3
CHS, KS, X	5	54	54
S, Z	4	4	4
CH, CK, C, G, KH, K, Q	5	5	5
MN, NM		66	66
M, N	6	6	6
FB, B, PH, PF, F, P, V, W	7	7	7
H	5	5
L	8	8	8
R	9	9	9

"Alternative" variants of letter combinations (used for multiple alternative codes generation):
CH → TCH
CK → TSK
C → TZ
J → DZH

Example

147740 → Iozefovich, Jacobovitch, Jacobovitz, Jacobowicz, Jacobowits, Jacobowitz, Josefovic, Josefowicz, Josifovic, Josifovitz, Josipovic, Josipovitz, Josofovitz, Jozefowicz, Yezafovich.
147750 → Iozefovich, Josefovic, Josifovic, Josipovic, Yezafovich.
345750 → Dashkovich, Djakovic, Djekovic, Djokovic.
783940 → Baldrick, Fielders, Walters, Weldrick, Wolters.
783950 → Baldrick, Weldrake, Weldrick, Welldrake.
964660 → Runchman, Runcieman, Runciman.
965660 → Runchman, Runcieman, Runciman.
596490 → Grancher, Greenacre.
596590 → Gehringer, Grainger, Grancher, Granger, Grangier, Greenacre, Grunguer.

This algorithm transforms about 5 surnames to the same code.

Subsequently Alexander Beider and Stephen Morse developed Beider-Morse Name Matching Algorithm, aimed to reducing the number of "false positive" values in Daitch-Mokotoff Soundex results with Jewish (Ashkenazic) surnames.

Metaphone

Metaphone (1990) algorithm has somewhat better efficiency. It has different approach to the encoding process: it transforms the original word using English pronunciation rules, so the conversion rules are much more complicated. The algorithm loses much less information, since the letters are not divided into groups. The final code is a set of characters 0BFHJKLMNPRSTWXY, but in the beginning of a word can also appear vowels from the set AEIOU.

Metaphone code computation algorithm

1. Remove all repeating neighboring letters except letter C.
2. The beginning of the word should be transformed using the following rules:
   KN → N
   GN → N
   PN → N
   AE → E
   WR → R
3. Remove B letter at the end, if it is after M letter.
4. Replace C using the rules below:
   With Х: CIA → XIA, SCH → SKH, CH → XH
   With S: CI → SI, CE → SE, CY → SY
   With K: C → K
5. Replace D using the following rules:
   With J: DGE → JGE, DGY → JGY, DGI → JGY
   With T: D → T
6. Replace GH → H, except it is at the end or before a vowel.
7. Replace GN → N and GNED → NED, if they are at the end.
8. Replace G using the following rules
   With J: GI → JI, GE → JE, GY → JY
   With K: G → K
9. Remove all H after a vowel but not before a vowel.
10. Perform following transformations using the rules below:
    CK → K
    PH → F
    Q → K
    V → F
    Z → S
11. Replace S with X:
    SH → XH
    SIO → XIO
    SIA → XIA
12. Replace T using the following rules
    With X: TIA → XIA, TIO → XIO
    With 0: TH → 0
    Remove: TCH → CH
    
13. Transform WH → W at the beginning. Remove W if there is no vowel after it.
14. If X is at the beginning, then replace X → S, else replace X → KS
15. Remove all Y which are not before a vowel.
16. Remove all vowels except vowel at the start of the word.

Examples

FXPL → Fishpool, Fishpoole.
JLTL → Gellately, Gelletly.
LWRS → Lowers, Lowerson.
MLBR → Mallabar, Melbert, Melbourn, Melbourne, Melburg, Melbury, Milberry, Milborn, Milbourn, Milbourne, Milburn, Milburne, Millberg, Mulberry, Mulbery, Mulbry.
SP → Saipy, Sapey, Sapp, Sappy, Sepey, Seppey, Sopp, Zoppie, Zoppo, Zupa, Zupo, Zuppa.

Same code is matched to 6 surnames in the average.

Double Metaphone

Double Metaphone (2000) differs a bit from other phonetic algorithms by generating from the original word two code values (both up to 4 characters) - one reflects the basic version of word pronunciation, another - an alternative version. It has large number of different rules that take into account origin of words, focusing on Eastern European, Italian, Chinese and another words. Transformation rules are sufficiently numerous, so everyone can read about this algorithm in the Dr Dobbs article.

Examples

APLF → Abelevitz, Abelov, Abelovitz, Abilowitz, Appleford.
APLT → Abelwhite, Abilowitz, Ablett, Ablewhite, Ablitt, Ablott, Appleton, Applewhaite, Applewhite, Epelett, Epilet, Eplate, Eplett, Euplate, Ipplett.
LPS → Labbez, Labes, Libbis, Llopis, Lopes, Lopez.
MKFX → Mackiewicz.
MKTS → Mackiewicz, Mccuthais, Mecozzi.
MTF → Mateev, Mathew, Mattevi, Mattheeuw, Matthew, Middiff.
M0 → Maith, Mathe, Mathew, Mathey, Mathie, Mathieu, Mathou, Mathy, Matthai, Mattheeuw, Matthew, Matthiae, Meth, Moth, Mouth.
SLFT → Salvador, Salvadore, Salvadori, Salvati, Salvatore, Slaughter.
XLFT → Slaughter.

Double Metaphone matches 8 or 9 surnames on the average to the same code.

Caverphone

Caverphone algorithm was developed in 2002 as part of one of New Zealand project to match the data in the old and new electoral lists, therefore it is most focused on a New Zealand pronunciation, but for foreign surnames ut gives quite acceptable results.

Caverphone code computation algorithm

1. Convert the first or last name to lowercase (the algorithm is case sensitive).
2. Remove letters e at the end.
3. Transform the beginning of the word using the table below (This is relevant only for New Zealand names). In this case digit 2 means temporary placeholder for a consonant letter, which will subsequently be removed.

   cough	rough	tough	enough	gn	mb
   cou2f	rou2f	tou2f	enou2f	2n	m2

4. Replace the letters using the table below:

   cq

   ci

   ce

   cy

   tch

   c

   q

   x

   v

   dg

   tio

   tia

   d

   ph

   b

   sh

   z

   2q

   si

   se

   sy

   2ch

   k

   k

   k

   f

   2g

   sio

   sia

   t

   fh

   p

   s2

   s

5. Replace all vowel at the word beginning with A, in other cases replace them with 3. So the digit 3 is a temporary placeholder for a vowel letter, that will be used in subsequent transformations and then will be removed. At the next step, it is necessary to replace using the following tables (the legend: s+ - group of consecutive letters, ^h - letter at the start, w$ - letter at the end):

   j

   ^y3

   ^y

   y

   3gh3

   gh

   g

   s+

   t+

   p+

   k+

   f+

   m+

   y

   Y3

   A

   3

   3kh3

   22

   k

   S

   T

   P

   K

   F

   M

   n+

   w3

   wh3

   w$

   w

   ^h

   h

   r3

   r$

   r

   l3

   l$

   l

   N

   W3

   Wh3

   3

   2

   A

   2

   R3

   3

   2

   L3

   3

   2

6. Remove all digits 2. If there is a digit 3 at the end 3, replace it with A. After that remove all digits 3.
7. Truncate the word to 10 letters or fill it to 10 letters with digit 1.

Examples

ANRKSN1111 → Henrichsen, Henricsson, Henriksson, Hinrichsen.
ASKKA11111 → Izchaki.
MKLFTA1111 → Maclaverty, Mccleverty, Mcclifferty, Mclafferty, Mclaverty.
SLKMP11111 → Slocomb, Slocombe, Slocumb.
WTLM111111 → Whitlam.

Caverphone matches about 4-5 surnames to the same code.

Conclusion

Most of these algorithms are implemented in a variety of languages, including C, C + +, Java, C # and PHP. Some of them, like Soundex and Metaphone, integrated or implemented as plug-ins for many popular databases, as well as used in the full-fledged search engines (for example, Apache Lucene). Their application is specific enough, because they are mostly suitable for surnames.

Links

1. Java source code for this article. Fuzzy-search-tools project on Google Code
2. Soundex, Refined Soundex, Metaphone, Double Metaphone and Caverphone Java implementations.
   Apache Commons Codec
3. NYSIIS Java implementation. Egothor project
4. Daitch-Mokotoff Soundex Java implementation. http://joshualevy.tripod.com/genealogy/dmsoundex/dmsoundex.zip
5. Soundex description. http://en.wikipedia.org/wiki/Soundex
6. Daitch-Mokotoff Soundex description. http://www.jewishgen.org/infofiles/soundex.html
7. NYSIIS description.
   http://en.wikipedia.org/wiki/New_York_State_Identification_and_Intelligence_System
8. Metaphone description. http://en.wikipedia.org/wiki/Metaphone
9. Double Metaphone description. http://www.drdobbs.com/article/184401251
10. Russian Metaphone description. http://forum.aeroion.ru/topic461.html
11. Caverphone description. http://en.wikipedia.org/wiki/Caverphone
12. Soundex online demo. http://www.gedpage.com/soundex.html
13. NYSIIS online demo. http://www.dropby.com/NYSIIS.html
14. Daitch-Mokotoff Soundex online demo. http://stevemorse.org/census/soundex.html
15. Metaphone online demo. http://www.searchforancestors.com/utility/metaphone.php