Fuzzy string search

Intro

Fuzzy search algorithms (also known as similarity search algorithms) are a basis of spell-checkers and full-fledged search engines like Google or Yandex. For example, these algorithms are used to provide the "Did you mean ..." function.

In this article I'll discuss the following concepts, methods and algorithms:

• Levenshtein distance
• Damerau-Levenshtein distance
• Bitap algorithm with modifications by Wu and Manber
• Spell-checker method
• N-gram method
• Signature hashing method
• BK-trees

I'll also perform a comparative test of the quality and efficiency of algorithms.

So...

Fuzzy search is a very useful feature of any search engine. However, its effective implementation is much more complicated than implementing a simple search for an exact match.

The problem of fuzzy string searching can be formulated as follows:
"Find in the text or dictionary of size n all the words that match the given word (or start with the given word), taking into account k possible differences (errors)."

For example, if you're requested for "machine" with two possible errors, find the words "marine", "lachine", "martine", and so on.

Fuzzy search algorithms are characterized by metric - a function of distance between two words, which provides a measure of their similarity. A strict mathematical definition of metric includes a requirement to meet triangle inequality (X - a set of words, p - metric):



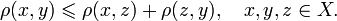
Meanwhile, in most cases a metric is understood as a more general concept that does not meet the condition above, this concept can also be called distance.

Among the most well-known metrics are Hamming, Levenshtein and Damerau-Levenshtein distances. Note that the Hamming distance is a metric only on a set of words of equal length, and that greatly limits the scope of its application.

However, in practice, the Hamming distance is useless, yielding more natural from the human point of view metrics, which will be discussed below.

Levenshtein distance

The Levenshtein distance, also known as "edit distance", is the most commonly used metric, the algorithms of its computation can be found at every turn.
Nevertheless, it is necessary to make some comments about the most popular algorithm of calculation - Wagner-Fischer method.
The original version of this algorithm has time complexity of O(mn) and consume O(mn) memory, where m and n are the lengths of the compared strings. The whole process can be represented by the following matrix:



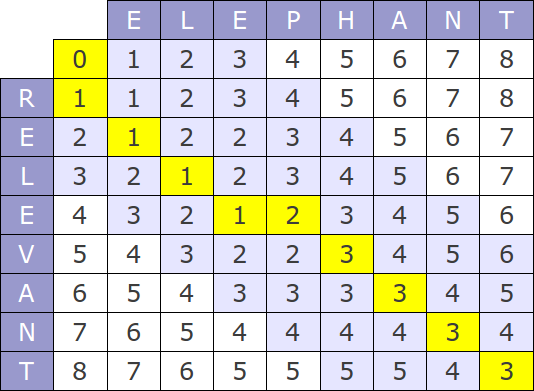
If you look at the algorithm's work process, it is easy to see that at each step only the last two rows of the matrix are used, hence, memory consumption can be reduced to O(min(m, n)).



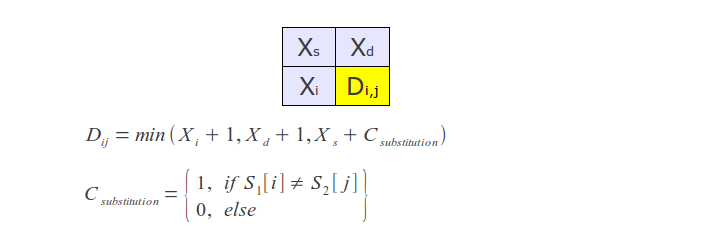
But that's not all - the algorithm can be optimized further, if no more than k differences should be found. In this case it is necessary to calculate only the diagonal band of width 2k+1 in matrix (Ukkonen cut-off), which reduces the time complexity to O (k min (m, n)).

Prefix distance

Usually it is necessary to calculate the distance between the prefix pattern and a string - ie, to find the distance between the specified prefix and nearest string prefix. In this case, you must take the smallest of the distances from the prefix pattern to all the prefixes of the string. Obviously, the prefix length can not be considered as a metric in the strict mathematical sense, what limits its application.

Often, the specific value of a distance is not as important as fact that it exceeds a certain value.

Damerau-Levenshtein distance

This variation contributes to the definition of the Levenshtein distance one more rule - transposition of two adjacent letters are also counted as one operation, along with insertions, deletions, and substitutions.
A couple of years ago, Frederick Damerau would ensure that most typing errors - transpositions. Therefore, this metric gives the best results in practice.



To calculate this distance, it suffices to slightly modify the regular Levenshtein algorithm as follows: hold not two, but the last three rows, and add an appropriate additional condition - in the case of transposition take into account its cost.

In addition to the above, there are many others sometimes used in practice distances, such as Jaro–Winkler metric, many of which are available in SimMetrics and SecondString libraries.

Fuzzy search algorithms without indexing (Online)

These algorithms are designed to search against previously unknown text, and can be used, for example, in a text editor, document viewers or web browsers to search the page. They do not require text pre-processing and can operate with a continuous stream of data.

Linear search

A simple one-by-one metric computation (eg, Levenshtein metric) for words of the input text. When you use metric limitation, this method allows to achieve optimum speed.
But at the same time, than more k, than more time grows. Asymptotic time complexity - O (kn).

Bitap (also known as Shift-Or or Baeza-Yates-Gonnet, and it's modifications by Wu and Manber)

Bitap algorithm and its various modifications are most often used for fuzzy search without indexing. Its variation is used, for example, in unix-utility agrep, which one functions like the standard grep, but it supports errors in the search query, and even provides a limited ability to use regular expressions.

For the first time the idea of this algorithm is proposed by Ricardo Baeza-Yates and Gaston Gonnet, the relevant article published in 1992.
The original version of the algorithm deals only with letter substitutions, and, in fact, computes the Hamming distance. But later Sun Wu and Udi Manber suggested a modification of this algorithm for computing the Levenshtein distance, ie brought support insertions and deletions, and developed the first version of agrep utility.

Bitshift operation

         

Insertions

Deletions

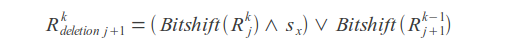
Substitutions

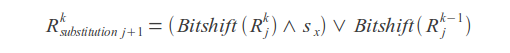
Result value


Where k - error count, j - letter index, s_x - letter mask (in mask one bits are placed at positions corresponding to the positions of this letter in the query).
Query match or mismatch is determined by the last bit of the result vector R.

High speed of this algorithm is ensured by the bit parallelism - calculations can be performed on 32 or more bits in a single operation.
In this case, a trivial implementation supports the search for the words shorten than 32 symbols. This restriction is caused by the width of a standard type int (32-bit architectures). We can use wider types, but it's usage may slow down the algorithm's work.

Despite the fact that the asymptotic time of this algorithm O (kn) equals linear method's time, it is much faster when the query is long and number of errors k more than 2.

Testing

Testing was performed on the text of 3.2 million words, average word length - 10.

Exact search

Search time: 3562 ms

Linear search using Levenshtein metric

Search time with k = 2: 5728 ms
Search time with k = 5: 8385 ms

Bitap with Wu-Manber modifications search

Search time with k = 2: 5499 ms
Search time with k = 5: 5928 ms

It is obvious that a simple iteration using the metric, in contrast to the Bitap algorithm, highly depends on the number of errors k.

At the same time, if we should search in constant large text, the search time can be greatly reduced by making text preprocessing (indexing).

Fuzzy search algorithms with indexing (Offline)

Feature of all fuzzy search algorithms with indexing is that the index is based on the dictionary compiled by the original text or list of records in a database.

These algorithms use different approaches to solve problem - some of them use reduction to exact search, while others use properties of metrics to construct various spatial structures and so on.

At the first step, we construct a dictionary using the original text, which would contain words and their position in text. Also, it is possible to calculate the frequency of words and phrases to improve search results.

It is assumed that the index, as well as dictionary, entirely loaded into memory.

Dictionary specifications:

• Source text — 8.2 Gb Moshkow's library (lib.ru), 680 millions of words;
• Dictionary size — 65 Mb;
• Word count - 3.2 million;
• Average word length — 9.5 letters;
• Average word square length — 10.0 letters;
• Russian alphabet (32 letters). Words that contain characters not in the alphabet, are not included in the dictionary.

Dependence of the dictionary size from the text size is not strictly linear - to a certain volume base word set is formed, between 15% on 500 thousand words and 5% on 5 million words, and then approaches a linear dependence, slowly decreasing and reaching 0.5% at 680 million words. Subsequent growth is ensured due to rare words.

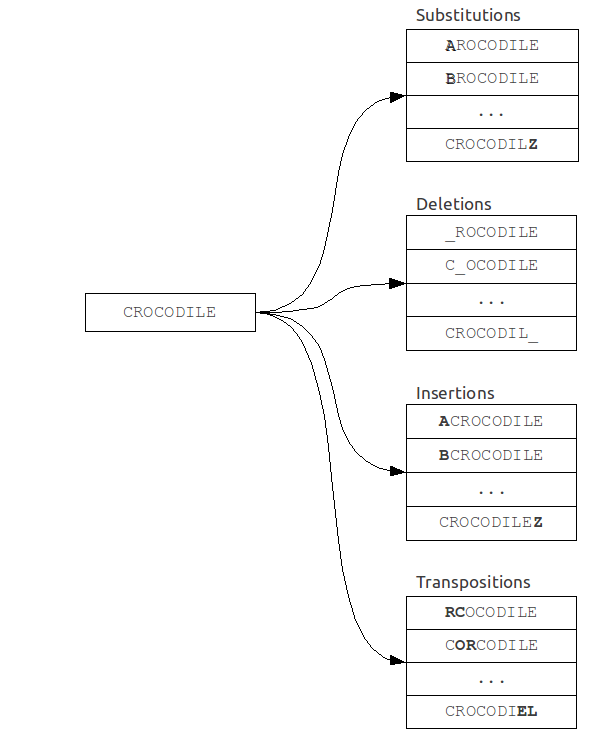
Spell-checker method

As the name implies, this algorithm is often used in spelling correction systems (ie, spell-checker systems), when the size of the dictionary is small, or else when speed is not the main criterion.
It is based on reducing the problem of fuzzy search to the problem of exact search.

A set of "mistaken" words is built from original query. Then every word from this set is searched in the dictionary for exact match.



Its time complexity is strongly dependent on the number of errors k and the alphabet size |A|, and for a binary search over the dictionary is:


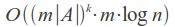
For example, in case of error count k = 1 and word length of 7 in the English alphabet set of misspelled words will have about 370 words, so we need to make 370 queries in the dictionary, which is quite acceptable.
But even at k = 2 the size of this set will be more than 75,000 words, which corresponds to a complete iteration over a small dictionary and, therefore, time is sufficiently large. In this case, we should not forget also that for each of such words are necessary to search for an exact match in the dictionary.

Specialties:

The algorithm can be easily modified to generate "mistaken" words using arbitrary rules and, moreover, does not require any dictionary preprocessing or additional memory.

Possible improvements:

We can generate not a whole set of "mistaken" words, but only those that are most likely to occur in real situations, like words with common spelling mistakes or typos.

N-gram method

This method was invented long ago, and is the most widely used because its implementation is relatively simple and it provides a reasonably good performance. This algorithm is based on the principle:

"If the word A matches with the word B considering several errors, then they will most likely have at least one common substring of length N".

These substrings of length N are named "N-grams".
At indexing step, the word is partitioned into N-grams, and then the word is added to lists that correspond each of these N-grams. At search step, the query is also partitioned into N-grams, and for each of them corresponding lists are scanned using the metric.



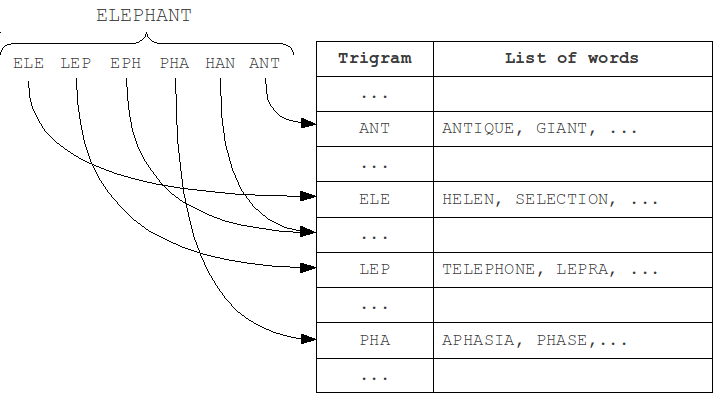
The most frequently used in practice are trigrams - substrings of length 3. Choosing a larger value of N leads to a limitation on the minimum length of words at which error detection is still possible.

Specialties:

N-gram algorithm doesn't find all possible spelling errors. Take, for instance, the word VOTKA (which must be corrected to VODKA, of course), and divide it into trigrams: VOTKA > VOT OTK TKA - we can see that all of these trigrams contain an error T. Thus, the word "VODKA" will not be found because it does not contain any of the trigrams, and will not get into their lists. The shorter the word and more errors in it, the higher chance that it won't contains in corresponding to query N-grams lists and will not appear in the result set.

Meanwhile, N-gram method leaves ample scope for using custom metrics with arbitrary properties and complexity, but there remains a need for brute force of about 15% of the dictionary.

We can separate N-gram hash tables by position of N-gram in the word (first modification M1). As the length of a word and the query can't differ by more than k, and the position of N-grams in the word can't differ by more than k. Thus, we should check only table that corresponds to the N-gram position in the word, and k tables to the left and to the right, total 2k+1 neighboring tables.



We can even slightly reduce the size of iterating set by separating tables by word length, and, similarly, scanning only the neighboring 2k+1 tables (second modification M2).

Signature hashing

This algorithm is described in L. M. Boytsov's article "Signature hashing". It is based on a fairly obvious representation of the "structure" of the word as a bit word, used as a hash (signature) in the hash table.

When indexing, such hashes are calculated for each word and this word is added in the corresponding table row. Then, during the search the hash is computed for a query and set of adjacent hashes that differ from the query's hash with no more than k bits is generated. For each of these hashes we iterate over corresponding list of words using the metric.

The hash computing process - for each bit of the hash a group of characters from the alphabet is matched. Bit 1 at position i in the hash means that there is a symbol of i-th group of the alphabet in the word. Order of the letters in the word is absolutely does not matter.



Single character deletion either does not change the hash value (if the word still have characters from the same group of the alphabet), or bit of corresponding group will be changed to 0. When you insert a similar manner or a bit of get up at 1 or no changes will be. Single character substitution a bit more complicated - the hash can either remain unchanged or will change in 1 or 2 bits. In case of transpositions there are no changes in the hash because the order of symbols at the hash construction does not matter as noted earlier. Thus, to fully cover the k errors we need to change at least 2k bits in the hash.



Average time complexity with k "incomplete" (insertions, deletions and transpositions, as well as a part of substitutions) errors:

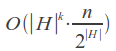
Specialties:

The fact that the replacement of one character can change two bits at a time, the algorithm that works with, for example, changing of 2 bits in hash, in reality won't return the full set of results because of lack of significant (depending on the ratio of the hash size to the alphabet size) amount of the words with two substitutions (and the wider the hash, the more frequently two bits will be changed at the same and the more incomplete set will be returned). In addition, this algorithm does not allow for prefix search.

BK-trees

Burkhard-Keller trees are metric trees, algorithms for constructing such trees based on the ability of the metrics to meet the triangle inequality: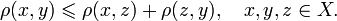



This property allows metrics to form the metric spaces of arbitrary dimension. These metric spaces are not necessarily Euclidean, for example, the Levenshtein and Damerau-Levenshtein metrics form a non-Euclidean space. Based on these properties, we can construct a data structure for searching in a metric space, which is Barkhard-Keller tree.

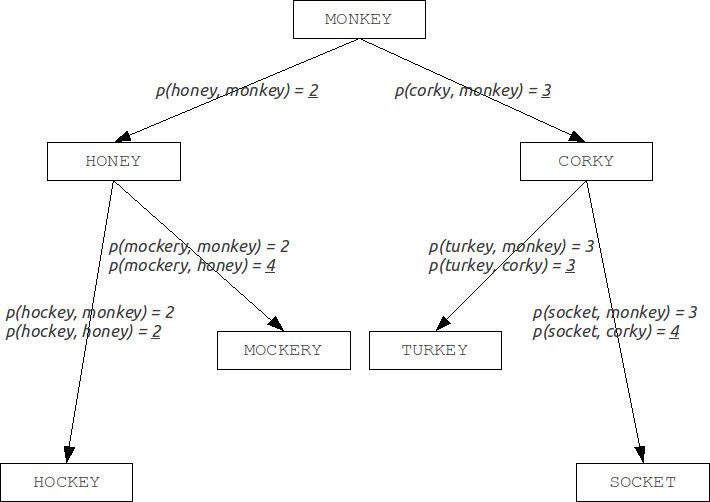
Improvements:

We can use the ability of some metrics to calculate the limited distance, setting an upper limit to the sum of the maximum distance to the node descendants and the resulting distance, which will speed up the process a bit: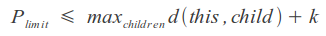

Testing

Testing was performed on a laptop with Intel Core Duo T2500 (2GHz/667MHz FSB/2MB), 2Gb RAM, OS — Ubuntu 10.10 Desktop i686, JRE — OpenJDK 6 Update 20.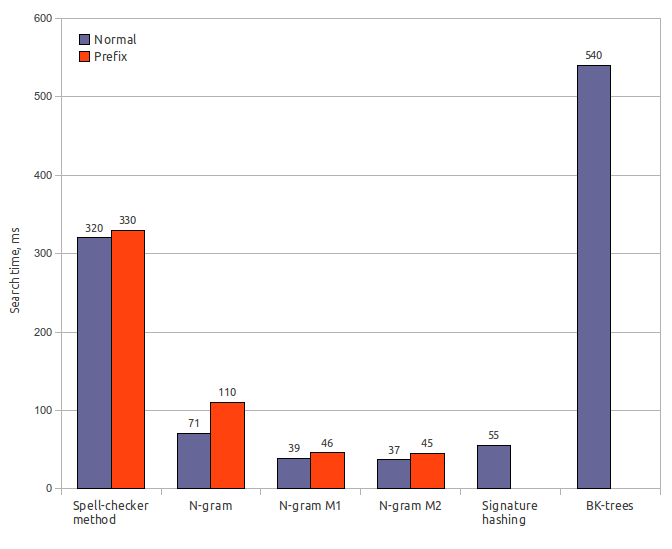



Testing was performed using Damerau-Levenshtein distance with error count k = 2. Index size is specified including dictionary size (65 Mb).

Spell-checker method

Index size: 65 Mb
Search time: 320 ms / 330 ms
Result recall: 100%

N-gram (original)

Index size: 170 Mb
Index creation time: 32 s
Search time: 71 ms / 110 ms
Result recall: 65%

N-gram (first modification)

Index size: 170 Mb
Index creation time: 32 s
Search time: 39 ms / 46 ms
Result recall: 63%

N-gram (second modification)

Index size: 170 Mb
Index creation time: 32 s
Search time: 37 ms / 45 ms
Result recall: 62%

Signature hashing

Index size: 85 Mb
Index creation time: 0.6 s
Search time: 55 ms
Result recall: 56.5%

BK-trees

Index size: 150 Mb
Index creation time: 120 s
Search time: 540 ms
Result recall: 63%

Conclusion

Most of fuzzy search algorithms with indexing are not truly sublinear (i.e., having an asymptotic time of O (log n) or below), and their performance usually depends on N. Nevertheless, multiple enhancements and improvements make it possible to achieve sufficiently small operational time, even with very large dictionaries.

There is also another set of various and inefficient methods, based on adaptations of techniques and methods from other subject areas to the current. Among these methods is the prefix tree (Trie) adaptation to fuzzy search problems, which I left neglected due to its low efficiency. But there are also algorithms based on the original approaches, for example, the Maass-Novak algorithm, it has sublinear asymptotic time, but it is highly inefficient because of the huge constants hidden behind asymptotic time estimation, which leads to a huge index.

The use of fuzzy search algorithms in real search engines is closely related to the phonetic algorithms, lexical stemming algorithms, which extract base part from different forms of the same word (for example, that functionality provided by Snowball), statistic-based ranking or the use of some complex sophisticated metrics.

This link http://code.google.com/p/fuzzy-search-tools takes you to my Java implementation of the following stuff:

• Levenshtein Distance (with cutoff and prefix version);
• Damerau-Levenshtein Distance (with cutoff and prefix version);
• Bitap (Shift-Or with Wu-Manber modifications);
• Spell-checker Method;
• N-Gram Method (with some modifications);
• Signature Hashing Method;
• Burkhard-Keller (BK) Trees.

I tried to make this code easy to understand, but effective enough for practical application. So enjoy.

It is worth noting that in the process of researching this subject I've made some own work, which allows to reduce the search time significantly due to a moderate increase in the index size and some restrictions on freedom of used metrics. But that's another cool story.

Links:

1. Java source codes for this article. http://code.google.com/p/fuzzy-search-tools
2. Levenshtein distance. http://en.wikipedia.org/wiki/Levenshtein_distance
3. Damerau-Levenshtein distance. http://en.wikipedia.org/wiki/Damerau–Levenshtein_distance
4. Shift-Or description with Wu-Manber modifications, in Deutsch. http://de.wikipedia.org/wiki/Baeza-Yates-Gonnet-Algorithmus
5. N-gram method. http://www.cs.helsinki.fi/u/ukkonen/TCS92.pdf
6. Signature hashing. http://www.springerlink.com/content/1aahunb7n41j32ne/
7. Signature hashing in Russian. http://itman.narod.ru/articles/rtf/confart.zip
8. Information retrieval and fuzzy string searching. http://itman.narod.ru/english/index.htm
9. Shift-Or and some other algorithms implementation. http://johannburkard.de/software/stringsearch/
10. Fast Text Searching with Agrep (Wu & Manber). http://www.at.php.net/utils/admin-tools/agrep/agrep.ps.1
11. Damn Cool Algorithms - Levenshtein automata, BK-tree, and some others. http://blog.notdot.net/2007/4/Damn-Cool-Algorithms-Part-1-BK-Trees
12. BK-tree Java implementation. http://code.google.com/p/java-bk-tree/
13. Maass-Novak algorithm. http://yury.name/internet/09ia-seminar.ppt
14. SimMetrics metric library. http://staffwww.dcs.shef.ac.uk/people/S.Chapman/simmetrics.html
15. SecondString metric library. http://sourceforge.net/projects/secondstring/